Примеры использования: diff (sin (x)^2), где diff — производная.
Одним из важных понятий в математическом анализе является производная функции, показывающая скорость изменения функции в заданной точке.
Пусть функция f (x) задана в интервале (a, b), в котором расположены точки х и х0. Функция изменяется, если меняется х. Разность значений х — х0 называется приращением (изменением) аргумента, записывается как Δx. Разность значений функции в двух точках называется приращением функции. Производная функции в точке f'(x) рассчитывается как предел отношения приращения функции к приращению аргумента, если последнее стремится к нулю.
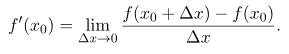 Каков смысл такого предела?
Каков смысл такого предела?
Геометрический смысл: производная в точке х0 равна угловому коэффициенту наклона касательной к графику функции y = f (x) в заданной точке.
Физический смысл: производная пути по времени равняется скорости прямолинейного движения.
Вычисление производной называется дифференцированием, а функция, имеющая производную в данной точке — дифференцируемой. Для нахождения производной функции пользуются таблицей с производными элементарных функций и правилами дифференцирования.
Правила дифференцирования
- При решении задач выражения следует упрощать. Константу выносить за знак производной.
- Производная суммы (разности) двух функций равна сумме (разности) их производных:
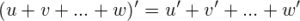
- производная произведения функций:
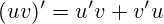
- производная от частного двух функций:
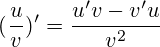
- производная сложной функции равняется произведению их производных:
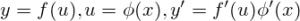
Таблица производных
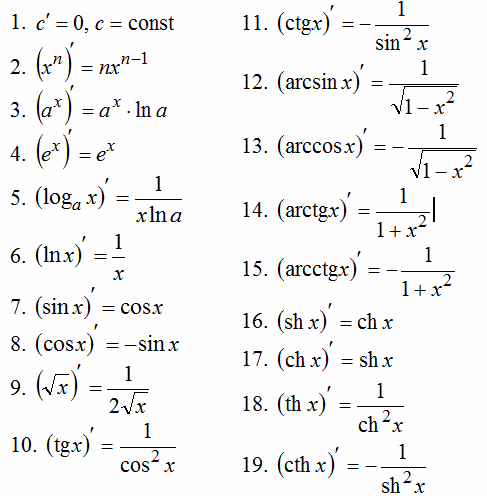
Онлайн калькулятор практически мгновенно совершит точно и достоверно любые вычислительные операции, как простые, так и сложные. Калькулятор производных поможет рассчитать производную онлайн от функции по заданной переменной с использованием аналитического дифференцирования. Для этого:
- введем математическое выражение с переменной х;
- в выражениях используем стандартные операции: + сложение, — вычитание, / деление, * умножение, ^ возведение в степень и математические функции;
- выберем порядок дифференцирования;
- жмем соответствующую кнопку;
- калькулятор выдаст подробное пошаговое нахождение производной.
